Efficient Digital Transformation - Particle Swarm Optimiser
- socialmediaemaildz
- Nov 17, 2021
- 5 min read
Updated: Nov 18, 2021
Digital transformation is most efficient when the leadership finds a right combination of technical tools and industry specifics.
Swarm Intelligence
You may call me easily excitable but I find it more than fascinating that we can mirror the swarm behaviour of birds, sheep or bees by mathematical functions and few lines of code in order to use this phenomenon for optimising e.g. machine learning models.
The basic principle of swarm intelligence is that a group of animals, like a flock of birds or a crowd of fishes that moves in a group does profit from the experience of each of its members. Hence the result of the group is much better than just the sum of the results of each individual member.
This is comparable to a group of dolphins hunting for food. Each member shares its experiences and findings so that the group itself is able to chase for the best options.

image by fgxrocks0 via pixabay.com
Business Environment
Pushing for the digital transformation in an enterprise, it is vital for the leadership to find the right combination of technical background, mathematical knowledge and industry expertise while — at the same time — taking care that the necessary cultural shift takes place.
Knowing what is around, how those tools, models and “state-of-the-art” applications are approximately working and when to use what under which circumstances builds up trust with those employees who have to work within the new technical environment but also gives more convenience and trust to those people who have to make the decisions.
Efficient data driven strategic decision making is the goal.
So, in the last article — in order to contribute to this goal — we shed some light on a technical aspect (reference below).
This time, we examine an example from the mathematical/ technical zone — the Particle Swarm Optimiser, as mirror of Swarm Intelligence.
Particle Swarm Optimiser - the Basis
A particle swarm optimiser is in principle an algorithm which was induced by the swarm intelligence behaviour of animals and -formally spoken- searches for the optimal solution in a solution space.
This could be the case of a machine learning model applied to classify observations into e.g. breast cancer/ non-breast cancer cases, default/ non-default credit applications or which is trained to predict the share price of certain stocks.
In this case, a lot of input parameters create a multidimensional solution space and the optimal solution is searched for by keeping the sum of errors in classifying/ predicting as low as possible. In other words, the cost function of the applied machine learning algorithm should be put at its minimum.
In case of the function below, this would be the dark blue zone.
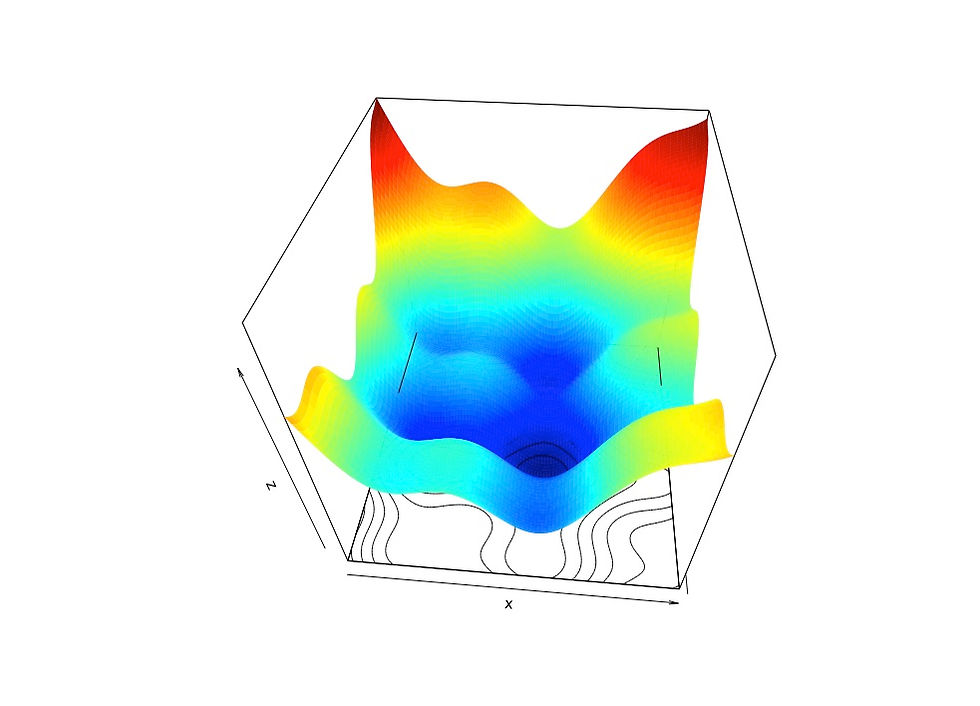
There are different strategies to find the optimal solution (in this case, the minimum of the cost function).
One of those strategies would be using gradient descent — algorithms. This optimisation algorithm — in short — tries to reach the minimum of the cost function by changing weights of the input parameters. The weight changing is done by taking into account the rate of change of the error. So, we are within the problem of calculus.
Though, the cost function may not only have one minimum. Instead there may be a lot of local minima (blue spots in the graph above) and one global minimum (the deep blue spot in the graph above).
Problem is that the gradient descent — algorithm may get stuck in one of the local minima which would represent a sub-optimal solution. You can find more details on this topic in some other articles. References are added below.
Particle Swarm Optimisers, on the other hand, try to get over these troubles by “sending out” random points uniformly distributed in the solution space. Then, for every random point the cost function value is derived.
And now, each random point (called particle) is moved in two directions:
- Towards the locally optimal (minimum) value for each point.
- Towards the globally optimal value across all points
With this step, swarm intelligence moves in. This moving of particles is of course repeated in several iterations.
Particle Swarm Optimiser - a bit more Detail
With every iteration, any of those single points searches for a minimum around its own location and at the same time is driven by the one minimum detected by the whole swarm.
At each iteration, every single particle would be updated as follows:

with

Given a 2-dimensional coordinate system (x, y), this would mean:

The velocity at iteration t+1 would be defined as:

with

As said before, this algorithm shall help to better overcome the problem of getting stuck in a local minimum. Besides, a particle swarm optimiser can be easily parallelised as each point can be updated in parallel and just the updated value of the point minimum as well as the swarm minimum is to be collected (e.g. important for map-reducing architecture).
Last but not least, the particle swarm optimiser does not depend on the gradient of the cost function which can be helpful when the gradient is difficult to derive.
Particle Swarm Optimiser - an Example
Let’s come back to the function featured in the graph above.
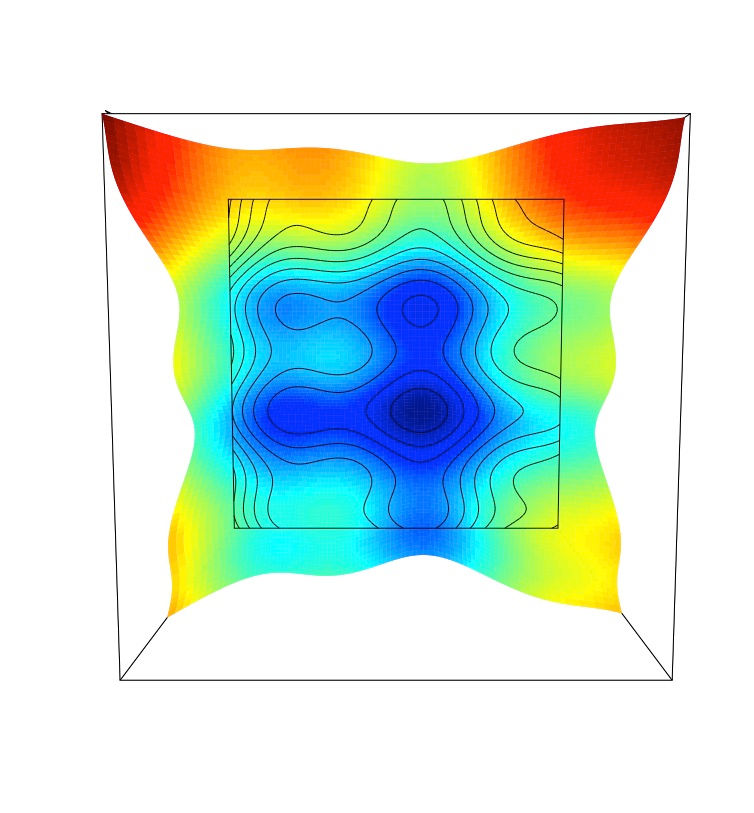
A view from on-top clearly reveals the local minima (blue zone) as well as the global minimum (deep blue zone) in this solution space:
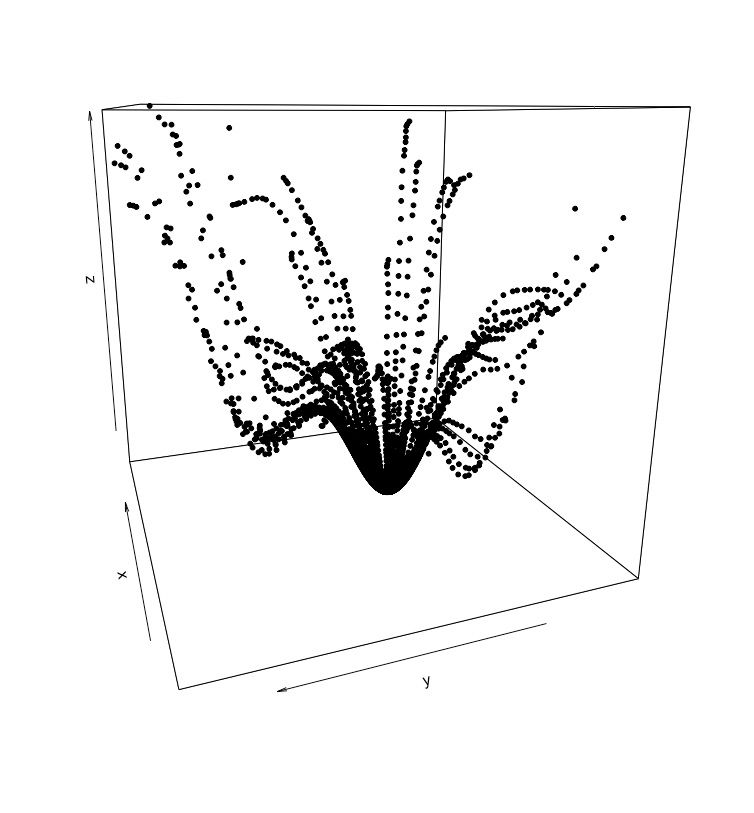
And here is the particle swarm optimiser at work! It shows the way of some 50 randomly distributed particles (in red) down to the global minimum within 100 iterations:

The next graph shows how those initially randomly distributed particles found their way into the global minimum from a 3D-perspective. Note, e.g. on the left side, how the algorithm did not get stuck in one of those local minima.
Finally, the overall result with particle swarm optimiser reaching the global minimum of a cost function in a 3-dimensional solution space:
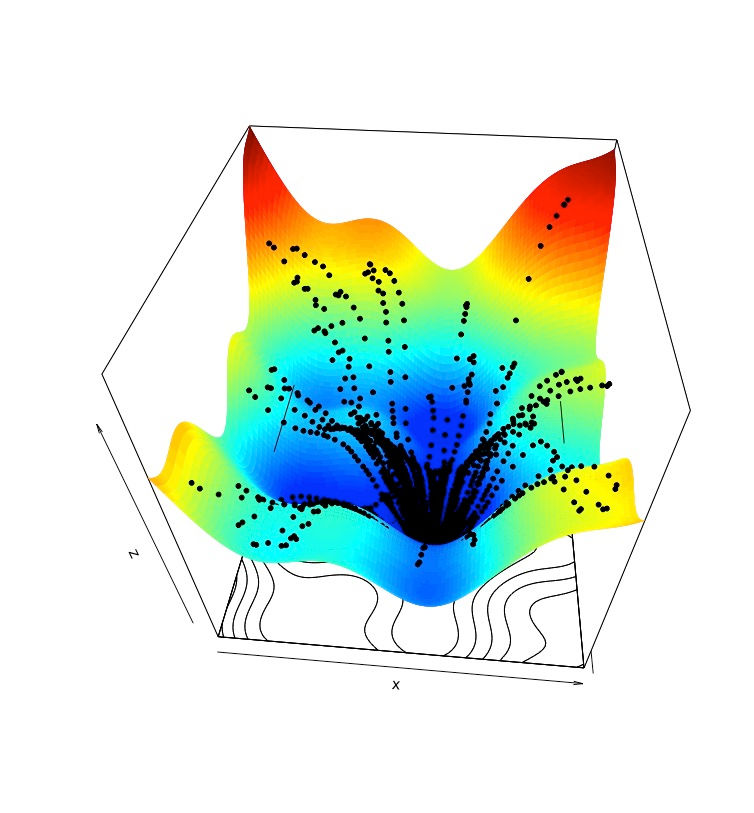
Conclusion
As I said in the beginning: It’s amazing!
Of course, this is just a very cautious touching the topic of Particle Swarm Optimisation. For more on this topic (together with some applications in the technical and financial field) I attached some references below.
Though, it shows that it is relatively easy to grasp the technical concept and the mathematical background in order to help to build up the necessary confidence and trust in those new technologies.
This helps a corporation to bring those technologies into the appropriate business context by combining it with fundamental business experience and hence, trigger the digital transformation.
Business context meets strategy meets new technology — the recipe for a corporation to stay ahead of the competition.
References
Efficient Digital Transformation — It Starts With The Small Steps by Christian Schitton published in Medium and Analytics Vidhya/ November 7, 2021
No Black Boxes In Machine Learning by D-DARKS published on LinkedIn/ August 3, 2021
New Generation in Credit Scoring: Machine Learning (Part 4) by Christian Schitton published on LinkedIn/ February 24, 2020
A Gentle Introduction to Particle Swarm Optimisation by Adrian Tam published in Machine Learning Mastery/ September 16, 2021
How to build a basic particle swarm optimiser from scratch in R by Riddhiman published in R’tichoke and Rbloggers/ October 12, 2021
Particle Swarm Optimization by Arga Adyatama published in RPubs/ December 27, 2019
Find optimal portfolios using particle swarm optimisation in R by Riddhiman published in R’tichoke and Rbloggers/ November 5, 2021


Comments